 |
La numération au cours
des temps
|
 |
| I Les babyloniens |
|
Chez les Babyloniens (
environ 2000 ans av.J.C. ), les symboles utilisés sont le clou
pour l'unité et le chevron pour les
dizaines. Le système est additif jusqu'à 60.
Clou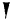 
Chevron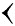 
Cette
numération est dite de position, car le nombre
dépend de la position des symboles utilisés
A partir de 60, la position des symboles entre en jeu de la
façon suivante :
|
204
|
7392
|
|
3 x 60 1 + 24
|
2 x 60 2 + 3
x 60 1 + 12
|
|
|
|
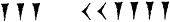
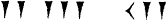
Comment comptaient-ils sur leurs doigts ?
Le pouce d’une main comptait les
phalanges des quatre autres doigts ( soit un maximum de 12 ) ;
une fois le maximum atteint, un doigt de l’autre main
« retenait » ce 12, si bien
qu’au total avec les deux mains, cela fait 5 x12 = 60.
|
| Q1 : écrire 182, 342 et 2001 en numération babylonienne : rédiger les
solutions sur le compte-rendu. |
|
|
| II Les égyptiens |
|
 Les
scribes égyptiens (environ 1800 av. J.C.)
représentaient 1 et les multiples de 10 par un
croquis : ci-contre les représentations des nombres
fractionnaires.
|
1
|
10
|
100
|
1 000
|
10 000
|
100 000
|
1 000 000
|
|
|
|
|
|
|
|
|
| |
|
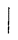
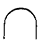
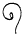
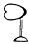
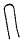
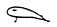
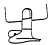
Corde enroulée
|
Fleur de lotus
|
Doigt coupé
|
tétard
|
Dieu assis
|
Pour lire un nombre, on additionne la valeur de
l'ensemble des symboles utilisés dans son
écriture :
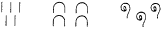 signifie 5 + 40 +
300 = 345
|
|
Q
2: Cette numération est-elle une
numération de position ?
Q 3 : écrire 210, et enfin 2001 en numération égyptienne : rédiger sur le compte
rendu
|
|
|
| III Les Mayas |
|
 La
civilisation maya s'étend vraisemblablement de 1500 av
JC à nos jours avec une apogée vers l'an
800 de
notre ère. Les signes de l'arithmétique et du
calendrier
(aussi précis que notre calendrier actuel) ont
été
assez vite connus. Mais le sens de la plupart des textes nous
échappe encore, et on ne parvient pas à trouver
la
clé qui permettrait de les traduire.
Les chiffres (glyphes)
représentent des têtes de divinités
vues de profil. Il y en a vingt : de zéro à
dix-neuf. Les Maya avaient en effet adopté une
numération vigésimale, dans laquelle les
unités vont en croissant ou en décroissant de
vingt en vingt : ils s'étaient rendus compte qu'en se
penchant un petit peu, ils pouvaient compter aussi sur leurs orteils,
d'où l'adoption de la base vingt.
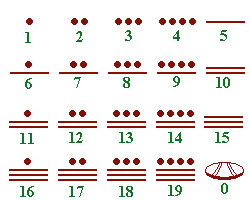
| Prenons
par exemple, Le nombre 20 s'écrit donc ainsi: |
 |
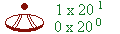le nombre 643
:
|
|
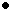
1 x
202
|
400
|
|
|
12 x
201
|
240
|
|
|
3 x 200
|
3
|
| |
Total
|
643
|
La civilisation Aztéque
éphémère (1168, émergence
de cette tribu à 1520, arrivée de Cortes le
conquistadore ) utilisa aussi la numération de base 20, mais
moins élaborée : un point pour une
unité, un fanion pour 20, trois fanions pour 60, une branche
pour 400.
|
Q
4 : écrire les nombres 264 en
numérotation maya
Q 5 : ecrire en décimal le nombre maya suivant:
|
|
|
| IV Les chinois |
|
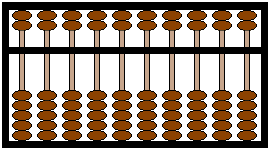
Dans le boulier chinois,
chaque
tige porte deux boules qui valent cinq (en haut) et cinq boules qui
valent un (en bas).
|
| Les boules
rapprochées du centre sont seules comptabilisées.
Ci-contre la valeur affichée est: 1 x 5 + 2 x 1 = 7.
Q
6 : quels système de numération vus
précédement utilise, comme le boulier, deux
symboles pour écrire tous les chiffres (sauf le
zéro)
Q 7 : faire un schéma du chiffre neuf
|
|
|
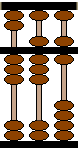
Le boulier fonctionne comme un
système de numération de position à
base dix. Le chiffre indiqué à droite correspond
aux unités.
Q
8 : Quel est le nombre
affiché ci-dessous?
Le boulier est très
pratique pour réaliser des additions ou des soustractions.
Q9 : Réaliser les schémas du boulier affichant
les
nombres 386 puis 153. Enfin, en utilisant uniquement ces
schémas (sans calcul) afficher le résultat de la
somme 386 + 153 sur un
autre schéma de boulier. (cliquer pour voir le
déroulement du calcul)
|
| V La numération en base 10 |
|
Dans la vie courante, nous
pratiquons la
numération décimale reposant à
l'origine sur nos
dix doigts : les dix symboles
chiffres permettent de représenter
tous les
nombres.
La
position des chiffres est primordiale dans cette
représentation (numération de position)
: il y a
quelques années
déjà,
vous avez appris ce qu'étaient les unités
(colonne de
droite), les dizaines, les centaines, etc.
Ainsi
on peut écrire 4138
comme 4 x 1000 + 1 x 100 + 3 x 10 + 8 x 1
On
remarque les égalités suivantes :
1000 = 103 ; 100 =102
; 10 = 101 ; 1 = 100
Donc
4138 peut s'écrire :
4 x 103 + 1 x 102 + 3 x 101
+ 8 x 100
10 est appelé BASE de cette numération (ici
décimale),
à chaque chiffre (compris entre 0 et 9) est soit celui des
unités, dizaines, etc
|
|
Q
10 : Ecrire 1101 en écriture détailler
de base 10
|
|
|
|
VI Des numérotations aux
ères numériques
|
| Deux
façons de compter sur ses dix doigts |
| La
méthode additive |
Avec
la numération de position |
Pour
montrer la valeur 37, on peut présenter trois fois de suite
ses mains avec les doigts levés, ce qui signifie 3 fois 10,
puis on montre les deux mains avec sept doigts levés.
|
On
convient alors de dire qu'un doigt baissé compte
zéro, mais chaque doigt levé
représente le chiffre un et compte une valeur qui
dépend de sa position.
 On
utilise alors la base deux. |
|
Q
11 : Que faudrait-il faire pour indiquer le nombre 245 selon la méthode de position (base 2) ? 10
Q
12 : Quelle est la valeur indiquée ci-dessous ?
Q
13 : Quel est le plus grand nombre qui puisse être représenté par les doigts des deux mains en base 2 ?
|
| Les
numérations de l'électronique et de la photonique |
En
électronique (courants électriques), ou en
photonique (lumière), il n'existe que deux états:
Tension
1 |
Lumière
1 |
| Pas de tension
0 |
Pas de lumière
0 |
|
une fois cette page terminée rendez sur la page suivante pour apprendre le codage binaire.
|
