|
Codage de l'information en binaire et hexadécimale |
Objectif : On se propose, après avoir présenté les supports d'enregistrement des données informatiques, d'étudier les systèmes de numération en binaire.
Chaque groupê d'élèves devra rédiger un compte-rendu en utilisant le traitement Star Office (dossier MPI du bureau de windows). Sur le compte rendu on rédigera les réponses aux questions posés de ces page HTML en justifiant chaque affirmation.
A. Les unités de stockages : disques durs, cédéroms, etc....
Objectif: connaître les supports d'enregistrement des données informatiques.
I Unités de mémoire
Un ordinateur possède plusieurs types de mémoires. On s'intéresse ici aux supports qui permettent un stockage de l'information en quantité importante. Cette information peut être conservée entre deux utilisations de l'ordinateur. Cette mémoire, appelée mémoire de masse, est stockée sur des disques ou des bandes papier que l'on peut conserver.1) Quelles mémoires de masse connaissez-vous?
L'unité d'enregistrement est le BIT, constitué par un chiffre zéro ou un chiffre un.
![]()
Cependant, pour coder une information, on utilise l'octet, constitué de huit BITS.
![]()
![]()
La quantité d'information présentes sur un disque se mesure en octets.
Comme un fichier comporte un grand nombre d'octets, on utilise des multiples de l'octet:
- le kilooctet: 1 Ko = 210 octets,
- le mégaoctet: 1 Mo = 220 octets,
- le gigaoctet: 1 Go = 230 octets.
2) Calculer, en octets, la valeur du kilooctet. Quelle remarque faites-vous?
3) Calculer, en octets, la valeur du mégaoctet. Quelle remarque faites-vous?
4) Calculer, en octets, la valeur du gigaoctet. Quelle remarque faites-vous?
II Les disquettes
| Les disquettes
contiennent un disque en plastique souple protégé
par un étui.
Les disquettes sont des supports magnétiques. Cela signifie que leur surface est aimantable et peut ainsi mémoriser des zéros et des uns.
1) Connaissez-vous d'autres supports magnétiques utilisés ailleurs qu'en informatique? |
|
| -
Démonter une disquette défectueuse: observer le
disque magnétique en
plastique souple sur lequel s'inscrivent les données (octets
composés
de 8 zéros et 1).
Elles sont double face. L'inscription HD indique Haute densité. HD Haute Densité: 80 pistes, 18 secteurs (1 474 560 octets ) Chaque piste, du fait des secteurs, est donc divisée en 18 blocs pouvant contenir 512 octets 2) Vérifier par le calcul la capacité d'une disquette HD. |
|
3) Faire un
copier coller du schéma ci-contre dans votre compte rendu
puis inscrire la légende:
Le début de la disquette est réservée à la "FAT", sorte de table des matières permettant de retrouver facilement tous les fichiers de la disquette. |
|
III Les disques durs
| Le disque
dur,
comme son nom l'indique, est rigide, au contraire de la disquette. Sa
surface est capable de s'aimanter et par là même
d'enregistrer les
zéros et les uns
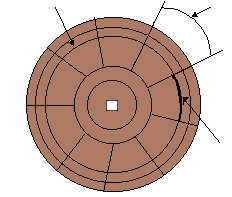
Pour des raisons d'encombrement et de rapidité de lecture, le disque dur comporte plusieurs plateaux superposés avec une tête de lecture (et d'écriture) sur chaque face. Lorsque le disque tourne, la tête de lecture frôle la surface du disque à moins d'un micromètre pour en lire les données. Les poussières pourraient occasionner des dégâts en détruisant localement la surface du disque. Le disque dur est dans une boîte bien étanche. Les disques durs ont vu leur capacité passer de 20 Mo à 20 Go en moins de 10 ans. Combien de plateaux et de têtes de lecture comporte le disque dur ci-contre ? |
|
| Comme pour
la disquette, le disque dur est formaté
pour y délimiter les pistes,
secteurs et blocs
qui permettent de localiser les données.
Les fichiers peuvent être enregistrés en plusieurs parties sur le disque dur. On dit alors qu'ils sont fragmentés. Si beaucoup de fichiers sont fragmentés, le temps de lecture est augmenté. Il est alors nécessaire de "défragmenter" le disque dur. Le temps d'accès aux données est d'environ 10 ms pour un disque dur, ce qui signifie que le bras de lecture met 10 ms pour se positionner. Le débit d'un disque dur est fonction de la vitesse de rotation et de la densité des informations du disque dur. On améliore cette densité par la qualité des têtes de lecture et d'écriture . |
|
IV Les Cédéroms
| Les
cédéroms ne sont pas, contrairement aux
disquettes et disques durs, des supports magnétiques.
Ils comportent une piste unique. La zone où se trouve la piste, large de 37 mm, décompose la lumière.
|
|
|
Leur surface est parcourue par une piste de lecture qui comporte une alternance de trous et de surfaces planes. La lecture se fait par un petit faisceau LASER. Ce dernier est réfléchi s'il arrive sur une portion plane de la piste (1) et dispersé s'il parvient sur un trou (0). La surface est métallisée pour bien réfléchir le faisceau.
La piste a une largeur de 0,5 mm et chaque bit codé correspond à un trou (0) ou une surface lisse (1) de 0,83 mm. Les cédéroms contiennent 650 Mo ou 700 Mo. |
|
|
Le
Cédérom défile et le faisceau LASER
permet sa lecture, bit par bit. Le procédé
s'apparente à du "morse
optique". |
|
V Les disquettes ZIP
| Les disquettes de 1,4 Mo sont
bien souvent insuffisantes pour transférer des
données d'un ordinateur à l'autre.
Les lecteurs "zip" fonctionnent avec des disquettes de 100 Mo ou 250 Mo. Ces lecteurs peuvent être externes et donc transportables. Les disquettes peuvent être effacées comme des disquettes ou disques durs habituels. Combien de disquettes de 1,4 Mo faut-il pour remplacer une disquette de 100 Mo ? |
|
B. Le codage de l'information en binaire
I Numération décimale
- La numération décimale utilise 10 chiffres:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
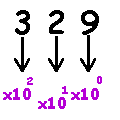
L’écriture du nombre 329 se traduit par 329 = 3x100 + 2x10 + 9x1= 3x102 + 2x101 + 9x100.
Écrire une égalité semblable pour les nombres 2 134 et 805.
| II
Numération binaire
L’informatique utilise des courants électriques, des aimantations, des rayons de lumière... Chacun de ces phénomènes met en jeu deux états possibles:
|
Il suffit de deux chiffres
pour traduire ces états: c’est la
numération binaire qui utilise les chiffres 0 et 1.
Un rayon de lumière peut parfaitement traduire ces deux valeurs:
|
Le nombre binaire 1 1 1 1 se traduit par :
| binaire | 1 | 1 | 1 | 1 |
| décimal | 23 | 22 | 21 | 20 |
1111 : 1.23+ 1.22 +1.21 +1.20= 8 + 4 + 2 + 1 = 15
Le nombre binaire 1 0 1 1 0 se traduit par :
| binaire | 1 | 0 | 1 | 1 | 0 |
| décimal | 24 | 23 | 22 | 21 | 20 |
10110 : 1.24 + 0.23 + 1.22 + 1.21 + 0.20 = 16 + 0 + 4 + 2 + 0 = 22
a) Compter en binaire jusqu'au nombre 11.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 000 | 001 | 010 |
b) Traduire en nombres décimaux les nombres binaires: 1 0 1 0 1 0 et 1 1 0 0 1 1 0 1 .
Chaque chiffre binaire (0 ou 1) se nomme BIT (de BInary digiT).
c) Combien de bits comporte le nombre binaire: 1 0 1 1 1 0 1 0 ?
d) Calculer son équivalent décimal.
Un nombre binaire de huit chiffres est un octet. (octo = huit)
e) Quelle est le plus grand nombre que l'on peut écrire avec un octet ? le plus petit ? Calculer leurs valeurs décimales.
f) Combien de nombres différents peut-on écrire avec un octet?
On peut aussi convertir un nombre décimale en binaire. Il suffit de faire une division par 2 jusqu'à ce que le quotient soit égale à 0. Le nombre binaire correspond aux restes de chaque division en partant de la fin.
| Exemple : 98 s'écrit 1100010. | 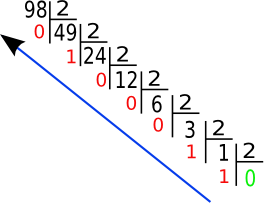 |
g) Écrire en nombre binaire les nombres décimaux suivants : 135 ; 57 et 74
h) En utilisant la calculatrice scientifique intégré à Windows (menu démarrer / programmes / accessoires), vérifier l'exactitude de tous vos résultats précédemment calculés.
III. La numération hexadécimale
La numération hexadécimale utilise 16 chiffres:| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
La numération hexadécimale compte 16 chiffres, c'est donc une base 16.
Le chiffre "A" hexadécimal correspond au chiffre "10" en décimal. Pour distinguer un nombre hexadécimale d'un nombre décimal, on le précède du signe $ (ex : $1A et $22 sont deux nombres hexadécimaux)
1) Donner, sous forme de tableau, l'équivalent décimale des chiffres hexadécimaux compris entre $0 et $14.
Pour trouver l'équivalent décimal du nombre $53A, il faut l'écrire sous la forme d'une somme de puissance de 16 :
| hexadécimale | 5 | 3 | A |
| décimal | 162 | 161 | 160 |
Au total, on a donc $53A qui vaut 5.162+3.161+10.160=1280+48+10=1338
2) Traduire en nombre décimal chacun des nombres hexadécimaux $111 ; $2A ; $B8C ; $5F0A.
Pour convertir un nombre décimale en héxadécimale, on passe par une valeur binaire. Par exemple, convertissons 226 en héxadécimale.
| décimale | 226 | |||||||
| binaire | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1×23 | 1×22 | 1×21 | 0×20 | 0×23 | 0×22 | 1×21 | 0×20 | |
| 14 |
2 | |||||||
| héxadécimale | E | 2 | ||||||
3) En utilisant la démarche précédente, traduire en nombre hexadécimal chacun des nombres décimaux 181 et 267.
4) Vérifier vos résultas en utilisant la calculatrice de Windows
L'ordinateur stocke des informations dans des lieux qui s'appellent des cases mémoires. Chaque case mémoire possède une adresse qui est codé en hexadécimale (comme un code postal quand on envoie une lettre).
Exemples d'adresse : $B8AC et $000F
Le code kexadécimal est utilisé pour compresser des données exprimées en octet que l'on convertit en hexadécimal. On gagne ainsi de la place. Le codage héxadécimal est utilisé également pour les couleurs.
IV. Principe du codage des couleurs
Chaque couleur est obtenue à partir de trois couleurs de base: le rouge, le vert et le bleu.
1) Approcher votre oeil de l'écran sur la cellule blanche ci-dessous. Qu'observez-vous ?
L'observation précédente grossie à la loupe montre que le pixel est constitué des 3 couleurs de base et on a la forme suivante pour un pixel :
![]()
Chacune des trois couleurs a une luminosité plus ou moins forte qui est déterminée par la valeur d'un octet. Cette valeur de luminosité peut donc aller de : 0000 0000 à 1111 1111.
2) Combien de niveaux de luminosité sont possibles pour chaque couleur (rouge, vert ou bleu)?
Pour coder la couleur d'un pixel, il faut donc utiliser 3 octets qui définissent chacun la luminosité des couleurs rouge, verte et bleue. Trois octets sont bien longs à écrire : on préfère utiliser un nombre hexadécimal .
Pour coder la couleur d'un pixel, on utilise un nombre hexadécimal à 6 chiffres : les 2 premiers correspondent à la luminosité du rouge, les 2 suivants à celui du vert et 2 derniers au bleu (ex : avec une intensité maximale sur le rouge on a $FF0000)
3) Calculer le nombre de couleurs que l'on peut demander à l'aide du code hexadécimal à 6 chiffres. On peut raisonner en considérant que chaque couleur est codée par un octet ou à partir du code hexadécimal.
4) En informatique, une image peut se définir à l'aide de16, 256 ou 16 millions de couleurs. Dans quel cas sommes nous?